
"Nuestros limites solo estan en nuestras mentes"
Matelengua



Describe your image

Efectos Opticos ¡Observa!




Método para la resolución de problemas:
1. Identifica y entiende el problema.
2. Traza un plan, busca estrategias y alternativas de solución.
3. Ejecuta el plan, escoge una alternativa y lleva a cabo la estrategia.
4. Evalúa lo que has hecho, mira hacia atrás.
MATELENGUA DÉCIMO
Diagnósticos y Pruebas
Aquí encontrarás pruebas para grado décimo, desafía tus conocimientos, ponte a prueba y amplía tus competencias matemáticas.
Trigonometría
La Geometría nos enseña a relacionar los lados de un triángulo pero no lo hace con el valor de los lados respecto al valor de sus ángulos.
El fin primordial de la trigonometría es relacionar los lados de un triángulo con sus correspondientes ángulos, lo cual permite establecer fórmulas matemáticas que fácilmente nos deducen los valores sin necesidad de hacer dibujos con instrumentos que deben ser muy precisos
Hay cosas que la geometría con sus simples métodos, no puede resolver, por ejemplo: medir el ancho de un rió, calcular la altura de una montaña partiendo de la base, la trigonometría utiliza métodos distintos pero muy sencillos para darle solución a estos problemas.
Por esta razón estudiaremos a fondo el triángulo rectángulo y las relaciones que existen entre sus lados y sus ángulos a las cuales Llamaremos FUNCIONES TRIGONOMÉTRICAS.
También se verá como se aplican a otra clase de triángulos, como se pueden hallar los otros elementos, veremos cómo utilizar estos conocimientos para solucionar problemas en nuestras actividades cotidianas.
El dominio de las funciones trigonométricas es indispensable para el estudio de la Física, Cálculo, Ingenierías, entre otros, motivo por el cual daremos los conceptos básicos más importantes en forma clara y concisa.
Ángulos
Observa el vídeo con la definición de concepto de ángulo, posición normal y representación en el lenguaje natural. Haciendo clic en el Botón o en la imagen.
Te invito a realizar la Guía de Preconceptos, trabajarás en equipo y construiras tú mismo los conceptos. Aquí
Descubre lo que se esconde en cada botón, haciendo clic seguirás aprendiendo.
TEOREMA DE PITÁGORAS

Actualmente, no podemos asegurar con certeza que el verdadero origen del Teorema de Pitágoras pertenezca en su totalidad a Pitágoras pero lo cierto es que la propiedad de la proporcionalidad de los triángulos rectángulos fue un estudio realizado por Pitágoras así como su consiguiente demostración y aplicación.
Para aplicar su teoría, Pitágoras elaboró una ecuación conocida como la fórmula del Teorema de Pitágoras mediante la cual se expresaba que la suma del cuadrado de los lados menores de un triángulo rectángulo, es decir los catetos, era igual al cuadrado del lado, la hipotenusa, mayor del mismo triángulo. Gracias a ésta fórmula surgió el origen de la demostración del Teorema de Pitágoras consiguiendo aportaciones de grandes filósofos como la demostración del teorema de Pitágoras por Euclides y se reveló la proporción que guardan este tipo de triángulos.
El origen del Teorema de Pitágoras está ubicado en Mesopotamia y el Antiguo Egipto, pero durante el inicio de sus estudios no se conocía como tal. Por aquel entonces, en el Teorema de Pitágoras, se trataban temas de valores con las longitudes de los lados de los triángulos rectángulos, su proporcionalidad y se estudiaba el método para resolver los problemas relacionados con dichos triángulos.
Muchas de éstas referencias se encontraron a lo largo de la historia de la Teoría de Pitágoras, escritas en papiros, tablillas y paredes, pero no se hallaron suficientes datos como para dar con una fórmula que demostrará la relación entre los lados de los triángulos rectángulo con exactitud hasta que el matemático y filósofo Pitágoras de Samos pudo dar con la teoría perfecta para aplicar el Teorema de Pitágoras, por éste motivo el Teorema lleva el nombre.
Para entender un poco mejor la historia del Teorema de Pitágoras es necesario conocer que está relacionada con un gran número de descubrimientos y de avances importantes a lo largo de los años, sin embargo el origen de Pitágoras fue conocido como Teorema de Pitágoras gracias a la aportación de Pitágoras, quien tras años de estudio consiguió aplicar su teoría de la proporcionalidad entre los lados de un triángulo rectángulo.
Así pues, la historia de Pitágoras se resume en que fue un filósofo y matemático de la antigua Grecia que contribuyó de manera significativa en el avance de las matemáticas, la filosofía y la geometría. El filósofo fue el impulsor de la escuela pitagórica en el siglo VI a.C y gracias a la ayuda de los pitagóricos, aquellos que pertenecían a la escuela, consiguió el descubrimiento de lo que hoy en día conocemos como el Teorema de Pitágoras.
Calcula las razones trigonométricas con la calculador científica
Relaciones de un triángulo rectángulo . Teorema de Pitágoras
Aplicación de Teorema de Pitágoras (TP), Razones trigonométricas (RT): Descomposición de Vectores
Las calculadoras científicas permiten hallar las razones trigonométricas de un ángulo.
Por ejemplo:
Para calcular sen 30° digita:
Tecla Sin + 30+ EXE o igual = 0,5
Para hallar la cotangente, secante y cosecante, como son inversas.
Digita 1/(sin 30) EXE o = 2

lEY DE SENO Y LEY DE COSENO
TRIÁNGULOS RECTÁNGULOS NOTABLES
CIRCUNFERENCIA UNITARIA

Las funciones trigonométricas se pueden estudiar de dos formas: a partir de las relaciones de los ángulos y los lados de un triángulo rectángulo o a partir de la circunferencia unitaria como funciones de números reales.
Circunferencia Unitaria



Razones Trigonométricas Vs Funciones Trigonométricas
Aquí encuentras la explicación de las Razones Trigonométricas y su relación y diferenciación con las Funciones Trigonométricas, también las líneas trigonométricas y análisis de las funciones trigonométricas.
Revisa el vídeo y refuerza tus conocimientos.
Líneas Trigonométricas en el Primer y Cuarto Cuadrante

Todas las líneas son positivas


Función Par e Impar
Traslación y Dilatación de Funciones
Función Seno

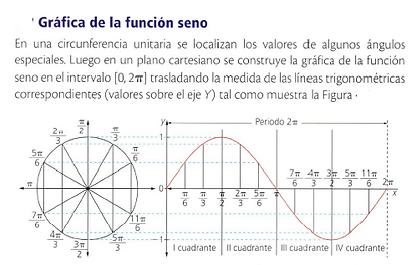

¡Vamos a jugar!

Relaciona las columnas y aprende más sobre las Funciones Trigonométricas
Funciones Trigonométricas
Función Coseno



Función Tangente




Función Cotangente



Función Secante



Función Cosecante




Identidades Trigonométricas

Aquí encontrarás como a partir de la circunferencia unitaria se demuestran las identidades trigonométricas fundamentales
Aquí encontrarás diferentes simplificaciones de las expresiones trigonométricas usando, según el caso, operaciones con fracciones, factorización y aplicación de las identidades trigonométricas fundamentales.
Geometría Analítica
Distancia entre dos puntos
Las Cónicas
Una sección cónica (o simplemente cónica) se presenta como las curvas en la intersección entre un cono y un plano; si dicho plano no pasa por el vértice.
Ellas son la elipse, la circunferencia, la parábola y la hipérbola.
Un cono circular recto de dos hojas con un plano que no pasa por su vértice
De acuerdo al ángulo y el lugar de la intersección es posible obtener circulos, hiperbolas , elipses o parabolas.
Cuando el plano solo toca uno de los mantos del cono y no es paralelo a una de sus aristas se obtiene una Elipse.
Cuando el plano corta los dos mantos del cono se obtiene una hiperbola.
Cuando el plano que corta es paralelo a una de las aristas del cono se obtiene una parábola.
























.jpg)



